HISTOGRAMA DE FREQUÊNCIA RELATIVA
Conceito: O histograma segundo Cooper e Schindler (2001) é uma solução convencional para apresentar dados de intervalo e de razão. O histograma é desenvolvido em forma de gráfico de barras, o qual mostra a variação sobre uma faixa específica, possibilitando expor e conhecer as características de um processo envolvendo a medição dos dados além de permitir ter uma visão geral da variação desse conjunto de dados.
Pode ser classificado de acordo com as seguintes características: o “histograma simétrico” ou de “distribuição normal” apresenta uma frequência mais alta no centro e que vai diminuindo conforme se aproxima das bordas, representando assim um processos estáveis e padronizados; o “histograma assimétrico” quando apresenta apenas um ponto mais alto (pico). O histograma geralmente, representa uma situação onde a característica de qualidade possui apenas um limite de especificação e é controlada durante todo o processo; O histograma denominado “despenhadeiro” que ocorre quando eliminados dados o que corresponde ao “corte” na figura, dando a aparência de que o histograma está incompleto; O “histograma com dois picos” costuma acontecer quando há uma mistura de dados diferentes; O histograma tipo “platô”, ocorre quando há diversas misturas de distribuições com médias diferentes; Finalmente o histograma “ilha isolada”, ou “retângulos isolados”, representa um situação onde certamente houve alguma anormalidade no processo decorrente de alguma falha, erro de medição, etc. (CÉSAR, 2011). Para que são usados: Segundo César, (2011) os Histogramas são utilizados para mostrar a frequência com que algo acontece, exemplo: em um caso como onde fosse necessário demonstrar graficamente de modo distribuitivo a altura de estudantes de um colégio, uma das maneiras mais adequadas para realizar isso seria
fazê-lo por meio de um histograma.
O Histograma, é uma ferramenta de qualidade, é um gráfico de barras verticais que apresenta valores de certa característica agrupados por faixas. É uma ferramenta útil para identificar um comportamento típico, permitindo a visualização de determinados fenômenos, dando uma noção da frequência com que ocorrem (CAMPOS, 1992).
Em primeiro lugar, poderíamos coletar estes dados e organizá-los em uma tabela para exemplifica-los e simplifica-los a leitura da coleta.
Exemplo: Conceito de César, (2011).
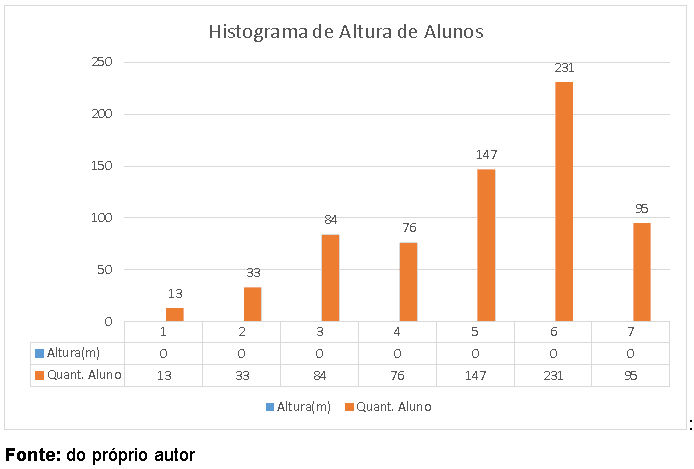
 Histograma da Altura dos Alunos (Fonte e Autoria: do próprio autor)
Histograma da Altura dos Alunos (Fonte e Autoria: do próprio autor)
Ao representarmos os mesmos dados do Histograma em formato de gráfico dos dados obtidos da tabela acima visualizaríamos as informações da seguinte forma:
Passos Para elaboração de um Histograma
Exemplo:
Uma escola pretende adquirir uniformes para seus 400 alunos. Como cada aluno possui diferente estatura, há necessidade de uniformes de diferentes tamanhos. Ao invés de medir a altura de todos os estudantes, o que levaria muito tempo e mão de obra, a escola pode tomar como medida utilizar como método estatístico, neste caso o histograma.
Primeiro procedimento: Determinação da amostra Uso da amostra aleatória, de forma que possa representar a totalidade dos alunos. Desta forma, a escola pode determinar um porcentual segundo Peinado, (2007) para designar traçar tamanhos variados que venham a atender de modo geral, proporcionalmente o tamanho de uniforme destes alunos.
Como isso pode ser feito?
Esta amostra pode ser feita de modo aleatório, de forma que possa representar a totalidade para vestimenta destes indivíduos. Desta, a escola pode optar por uma amostra de aproximadamente 55 estudantes, conforme apresentado no quadro a seguir.
Tabela esta que possa vir a representar um histograma da estatura de basicamente dos estudantes que frequentam a escola.
Segundo procedimento: Cálculo de Amplitude
Segundo César, (2011) amplitude de uma de dados numéricos é a diferença entre o maior e o menor valor dos dados obtidos, representada assim pela letra R. Ou seja, a amplitude é dada pela diferença da altura entre o aluno mais alto e o aluno mais baixo.
R=Maior valor – menor valor
R= 1,99—1,47=0,52m
Terceiro procedimento: Escolher o número de classes Definir o número de classes a qual será utilizado no Histograma, definir faixa de variação a qual será lançado no gráfico, a maneira de dispor os dados. Não existe
uma regra determinada para esta escolha. O número de faixas não deve ser muito grande, de forma a dispensar demasiadamente os dados; nem muito pequeno, de forma a descaracterizar o histograma. O número de classes depende do tamanho da amostra. O quadro abaixo mostra a quantidade de classes a ser utilizada na construção de um histograma, em função do tamanho da amostra de que se dispõe.
Determinação do número de classes
Ao utilizarmos uma amostra exemplo com 55 elementos, serão utilizadas 7 classes.
Quarto procedimento: Calcular o intervalo entre as classes
Este intervalo pode ser calculado dividindo a amplitude pelo número de classes,
usando o exemplo da formula a seguir:



 WhatsApp 11-99832-9604
WhatsApp 11-99832-9604